Niepewności pomiarów

Pomiary podzielić możemy na bezpośrednie i pośrednie. Pomiary bezpośrednie to takie, gdzie wynik pomiaru (np.: długość zmierzona suwmiarką) jest od razu wynikiem ostatecznym (nie trzeba dokonywać żadnych obliczeń na podstawie znajomości zależności między wartościami). Pomiar pośredni zaś wymaga dokonania obliczeń na podstawie wyniku i dodatkowo zazwyczaj wymaga dokonania kilku pomiarów bezpośrednich (np. pomiar oporu na podstawie napięcia i natężenia).

Każdy pomiar charakteryzuje się niepewnością, którą opisać można jako rozrzut wartości, który można rozsądnie przypisać do wyniku pomiaru i te podzielić możemy na maksymalną (nie wykorzystywaną już dzisiaj), standardową oznaczaną jako uc(x) oraz rozszerzoną oznaczaną jako Uc(x).

Niepewność standardowa

Wyrażona jest w formie odchylenia standardowego a obliczyć możemy ją przy pomocy metody typu A oraz typu B. Ta pierwsza stosowana jest wówczas gdy mamy doczynienia z serią pomiarów i wyznaczamy ją na drodze analizy statystycznej. Jeżeli założymy, że rozkład prawdopodobieństwa wyniku (xi) przyjmuje postać krzywej Gaussa jako wynik pomiarów przyjmujemy średnią arytmetyczną.

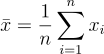
wzór na średnią \bar x=\frac{1}{n}\sum_{i=1}^{n}{x_i}

Zaś niepewność standardową wyniku oblicza się według poniższego wzoru nazywanego odchyleniem standardowym wielkości średniej.

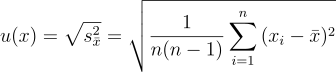
wzór na niepewność standardową typu A \sum^{n}_{i=1}{(x_i-\bar{x})^2}

Metoda typu B wykorzystywana jest wówczas gdy dokonujemy pojedynczego pomiaru lub wyniki nie wykazują rozrzutu. Można wyznaczyć ją na podstawie niepewności wzorcowania opisywanej jako Δx lub niepewność graniczna. Określana jest ona przez producenta lub na podstawie wartości działki elementarnej przyrządu pomiarowego (wtedy zwykle przyjmuje wartość pojedynczej działki elementarnej przyrządu).

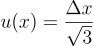
niepewność wzorcowania u(x)=\frac{\Delta x}{\sqrt{3}}

Drugą przyczyną niepewności typu B jest niepewność eksperymentatora Δxe, która to szacowana jest na podstawie umiejętności eksperymentatora oraz sposobu wykonywania pomiaru. Wyznacza się ją w sposób analogiczny jak niepewność wzorcowania. Jeśli te dwie niepewności występują jednocześnie sumuje się je w sposób przedstawiony niżej.

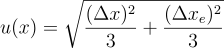
suma niepewności typu B u(x)=\sqrt{\frac{(\Delta x)^2}{3}+\frac{(\Delta x_{e})^2}{3}}

Gdy niepewność typu A oraz B występują jednocześnie to dodaje się je według poniższego wzoru, który należy jednak wykorzystywać wówczas gdy obydwie niepewności są tego samego rzędu wielkości.

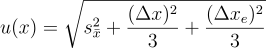
suma niepewności typu A i B u(x)=\sqrt{s^2_{\bar{x}}+\frac{(\Delta x)^2}{3}+\frac{(\Delta x_{e})^2}{3}}

Wszystkie wskazane wyżej metody dotyczyły pomiarów wykonywanych bezpośrednio jednak bardzo często jakiegoś wyniku z nie da się odczytać wprost i wówczas mamy doczynienia z pomiarem pośrednim, dla którego liczy się niepewność złożoną obliczaną według następującego wzoru jeśli mamy doczynienia z pomiarami nieskorelowanymi (czyli nie mierzy się ich w jednym pomiarze). Gdy mamy doczynienia z pomiarami skorelowanymi niepewność liczy się w sposób analogcziny jak w wypadku niepewności typu A.

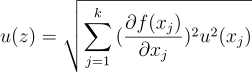
niepewność złożona u(z) = \sqrt{\sum^k_{j=1}{(\frac{\partial f(x_j)}{\partial x_j})^2}u^2(x_j)}

Niepewność rozszerzona

Niepewność standardowa określa przedział, w któym znajduje się wartość z 68% prawdopodobieństwem dla niepewności typu A i 58% dla niepewności typu B. Aby móc porównywać wyniki uzyskane w różnych laboratoriach i warunkach wporwadzono niepewność rozszerzoną. Pozwala ona na to, aby w ramach przedziału niepewności znalazła się przeważająca część wyników. Wzór na niepewność rozszerzoną przedstawiono poniżej.

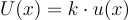
wzór na niepewność rozszerzoną U(x) = k \cdot u(x)

Współczynnik k we wzorze to współczynnik rozszerzenia, którego ustawienie na wartość 2 powoduje, że prawdopodobieństwo znalezienia się wartości w tym przedziale wynosi 95% a na 3 99% (z taką wartością współczynnika zwykle podaje się niepewność rozszerzoną w literaturze).

Źródła artykułu